Paso 1. Cambiar el modelo a forma estándar
Las desigualdades del tipo ≤ implican la cantidad no usada u holgura del
recurso. Para convertirla en una igualdad y hacer uso de ella en el método
simplex, se adiciona una variable holgura al lado izquierdo de la ecuación
(𝑆𝑛), de tal forma que:
6𝑋1 + 4𝑋2 ≤ 24
Se convertirá en
6𝑋1 + 4𝑋2 + 𝑆1 = 24
Por su parte una restricción del tipo ≥ representará un límite inferior para
las actividades a las que se encuentra sujeta la función objetivo; por lo
tanto, la cantidad por la que el lado izquierdo de la ecuación es mayor al
lado derecho o límite se considera un excedente y para convertirla en una
igualdad será necesario restar la variable de excedencia:
𝑋1 + 𝑋2 ≥ 800
Se convertirá en
𝑋1 + 𝑋2 − 𝑆2 = 800
Deberán ponerse tantas variables holgura como restricciones existan. Por su parte, la función objetivo deberá cambiar de signo (de positivo a
negativo y viceversa), de tal modo que.
𝑀𝑎𝑥 𝑍 = 100𝑋1 + 125𝑋2
Será:
𝑀𝑎𝑥 𝑍 = −100𝑋1 − 125𝑋2
De tal forma que el modelo estándar completo se escribirá así:
𝑀𝑎𝑥 𝑍 = −100𝑋1 − 125𝑋2
6𝑋1 + 4𝑋2 + 𝑆1 = 24
𝑋1 + 𝑋2 − 𝑆2 = 800
𝑋1, 𝑋2, 𝑆1 𝑆2 ≥ 0
Paso 2. Armar la tabla simplex
Los valores del modelo serán introducidos a la tabla simplex
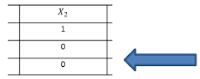
Observe que en la primer columna se han colocado las variables holgura (𝑆𝑛) y en las filas, de acuerdo a dicha variable, se coloca la restricción que corresponde y en la última fila (ó llamado también renglón objetivo) los valores de la función objetivo. Cuando las variables holgura no aparecen el valor que tomará será cero.
Paso 3. Elegir el valor de Z más negativo
En la fila donde aparecen los datos de Z (la función objetivo) habrá que localizar el valor más negativo excluyendo la última columna. La columna en dónde se encuentre dicho valor se denominará columna de entrada o columna de trabajo.
Paso 4. Determine la variable de salida y el pivote
Dividiendo cada número de la columna solución entre los valores de la columna entrada (a excepción del renglón objetivo). Entonces:
Del resultado, se elige el valor positivo más pequeño sin tomar en cuenta los valores negativos y a la intersección se le denominará pivote
Es muy importante que el pivote tome el valor 1; si no se tiene ese valor habrá que dividir el renglón objetivo entre el valor del pivote
Los nuevos valores se colocarán en la tabla simplex, en el renglón que corresponde; en este caso 𝑠1 retomará el valor de la variable en donde se encontró la columna entrada 𝑋2.
Paso 5. Hacer ceros los demás valores de la columna entrada
Para el ejemplo los demás valores que deben hacerse cero son 1 y – 125
Para eso habrá que multiplicar el renglón 𝑋2 por el inverso del valor que se hará cero y a este resultado se le sumará al renglón que desea convertirse (donde está el inverso), de manera más precisa:
El nuevo valor encontrado se asignará en el renglón que corresponde:
Como usted puede apreciar, los valores junto al pivote en la columna entrada se han convertido en ceros, señal de que hasta este momento se han hecho los cálculos correctos.
De la misma manera puede apreciar que en el renglón de Z ya no ha quedado ningún valor negativo, por lo tanto ya ha terminado el procedimiento.
